Rules

Probabilty Formula

Prob(E) ^|E|⁄_|S|

|E| = Total number of favorable outcomes

|S| = Total number of Outcomes or Sample space

Elementary Rules

The Elementary Addition Rule

Given E₁ and E₂ are disjoint:

Prob(E₁ ∪ E₂) = Prob(E₁) + Prob(E₂)

The Elementary Multiplication Rule

Given two independent events:

Prob(E₁ ∩ E₂ = Prob(E₁) * Prob(E₂)

General Rules

The General Addition Rule

Prob(E₁ ∪ E₂) = Prob(E₁) + Prob(E₂) - Prob(E₁ ∩ E₂)

If the events are disjoint, then E₁ ∩ E₂ = ∅

Which also means that the general addition rule will reduce to the elementary addition rule for probability.

The General Multiplication Rule

Prob(E₁ and E₂) = Prob(E₁) * Prob(E₂|E₁)

= Prob(E₂) * Prob(E₁|E₂)

Used when the events are not independent.

Complement

Prob(E') = 1 - Prob(E)

The complement E' of E is the event consisting of all the outcomes that do not occur in E.

Bernoulli Trials

Prob(k) = _nC_k p^k q^n-k

k = Desired outcome

n = # of trials

p = probability of success

q = probability of failure (also referred to as 1-p)

An experiment must satisfy the following to use the Bernoulli equation:

1) The experiment is repeated for a fixed amount of trials with each trial independent from others.

2) There are only 2 possible outcomes

3) The probabilty of success is the same for each trial.

4) A random variable counts the number of successful trials.

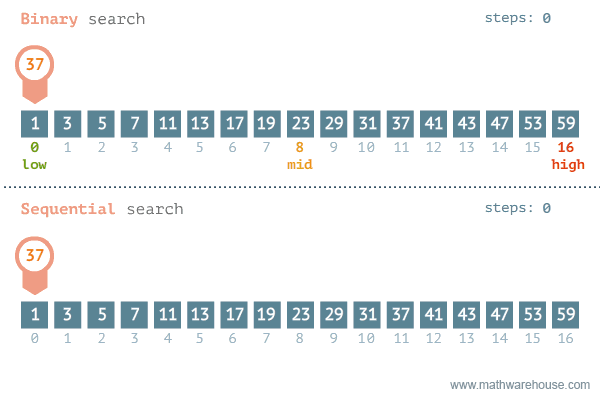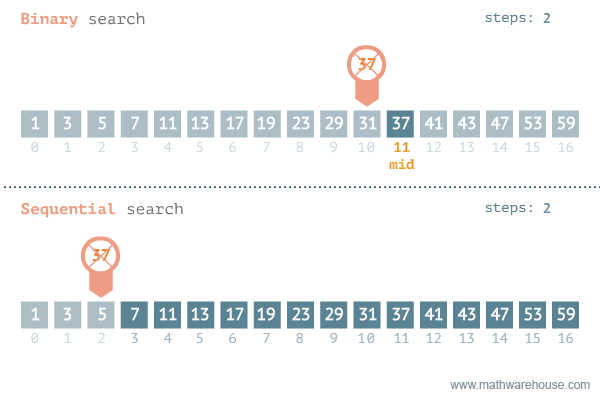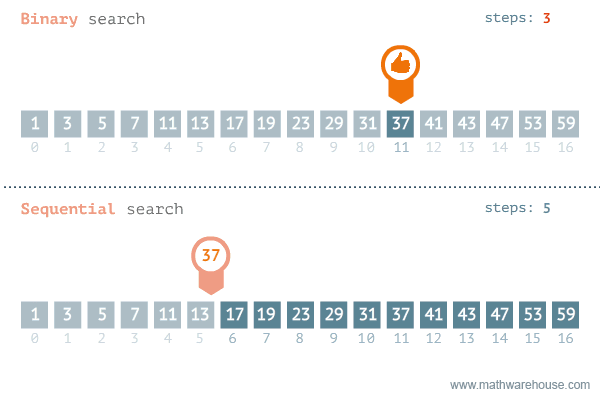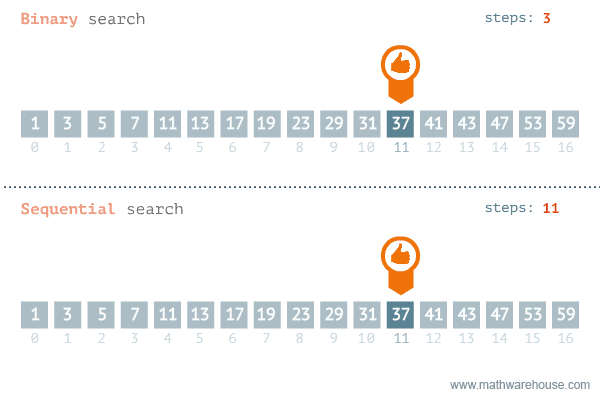
Binary Search

Only works if the numbers are in order.

Can be more effective than a standard linear search.

Less effective if the number searched is in the beginning of the list; sequential search is more effective then.

Binary search works by going to a middle number in a list.

Based on if the number being searched is higher or lower than the middle number in the list, it continues searching either the lower or higher half of the numbered list.